Disclaimer:

  1. 这几篇 paper reading 是我去年暑期在 MSRA 实习期间留下的笔记，近期整理文件翻出遂转至博客。其中的内容不保证正确性，观点仅供参考。
  2. “十问” 的格式来源于沈向洋老师的分享，指路 👉

1. 这篇文章究竟讲了什么问题？

  1. 蒙特卡洛可微渲染中的对偶采样
  2. 问题：
    1. 可微渲染：渲染是在3D场景中进行积分得到2D图片，可微渲染就是逆向渲染的一个方法，通过微分从2D图片得到3D场景的部分参数
    2. 本文主要研究的是 physical-based 可微渲染，不是光栅化那种的
    3. 传统的 sampling 方法在面对高光表面的时候，会非常低效，尤其是在对全局的几何求导的时候
    4. 引入对偶采样可以大幅提高采样效率

2. 这个问题的性质是什么？它的重要性何在？

  1. 对于传统方法的改进，解决掉了传统的 sampling 方法在面对高光物体时的低效问题
  2. 重要性：
    1. 计算制造、计算成像、遥感
      1. 不过感觉高光这件事在成像上重要一些，遥感这种远场的情况很少出现高光
    2. 完善了以往的方法，使得整个 BSDF 的对偶采样框架有更好的普适性

3. 这篇文章致力于证明什么假设？

利用了对偶采样的蒙特卡洛算法能够很好的估计内部积分，从而使得整个采样框架具有更好的效率和普适性

4. 有哪些与这篇文章相关的研究？这一领域有哪些关键人物？

  1. 本文的作者（Zhao Shuang）就是专门做可微渲染的，在去年的 SIGGRAPH20 上给了一个可微渲染的 course，CVPR21 又给了一个 tutorial talk
  2. Wenzel Jakob, 开发了 mitsuba2 的团队，mitsuba2 主要解决了可微渲染中高性能 auto diff 的问题
  3. 还有 Tzu-Mao Li 老师

5. 这篇文章提出的问题解决方案中，核心贡献是什么？

  1. 面对高光表面，蒙特卡洛为什么慢？

    1. When 𝐹 contains high-magnitude positive and negative regions, estimating 𝐼 using Monte Carlo methods with independent samples can suffer from very slow convergence.
    2. 简单说就是当被积分的函数包含尺度很大的正负区域的时候，蒙特卡洛方法很难收敛
    3. 而高光区域就是这个特点，所以难以快速收敛

  2. 如何加速蒙特卡洛采样？

    1. 如果被采样的函数是一个偶函数，那么一般采用对偶采样的方法，可以大大降低所需的样本数（因为样本的方差变小了）

  3. 为什么可以用对偶采样？

    1. 采样的函数需要是偶函数

    2. Our key observation is that geometric derivatives of BSDFs, under certain parameterizations, are approximately odd functions.

      1. 为什么呢？

        1. 首先作者使用的是一个 microfacet 的 BSDF 函数

          $$f_s(\omega_\text{i},\omega_\text{o})=D(\omega_\text{h})f_s^{(0)}(\omega_\text{i},\omega_\text{o})$$

          D 是正态分布函数，omega_h 是半向量

          将这个BSDF函数求导得到：

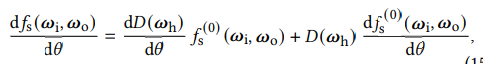
          Untitled.png

          其中的 $f_s^{(0)}$ 和 $d_{f_s}/d\theta$ 很少变化，而 D 在高光区域变化非常大

        因此作者提出：

        1. Beckmann、GGX 等常见模型里，D 都是对称的

        2. 而且在一个局部坐标系里，如果按照 z 轴对齐，D 更是偶函数了

          下图是他们对于这个 insight 可视化的结果

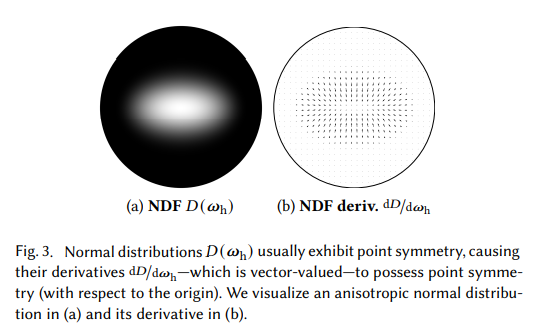
          Untitled%201.png

  4. 核心算法：

    Untitled%202.png

    注意：对偶采样只有在高光部分才会使用，这个是文章的 algorithm 2 主要表明的 idea

  5. 光路的对偶采样

    作者发现对偶采样技术可以适配到 path-level

    1. 单向 unidirectional

      就是在每个高光的地方做一次对偶，比如下图中就是p3和p4

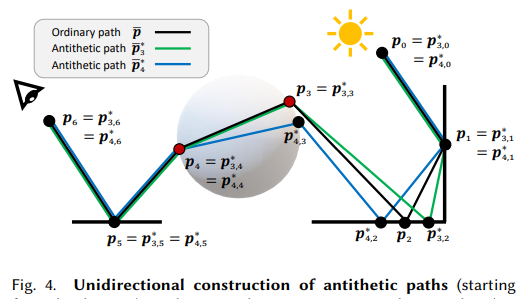
      Untitled%203.png

    2. 双向 bidirectional

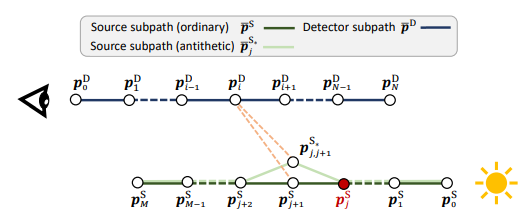
      Untitled%204.png

      通过对偶采样一个对偶的 source path 和一个对偶的 detector path（图里没画），然后普通的path 和对偶的 path 都要连起来

6. 实验是如何设计的？

  1. Differential rendering comparison

    可微部分，比较 Equal quality & Equal time 下的微分结果

    作者选用了 6 个带有高光的场景（4个各向同性的 BSDF，2个各向异性的 BRDF），并整合了 edge sampling、unidirectional、bidirectional 等技术，在上面对比使用和不使用对偶采样的效果

  2. Inverse-rendering comparison

    使用对偶采样得到的微分结果进行逆向渲染，在 bunny、杯子、爱因斯坦画像上进行逆向渲染。

7. 实验是在什么样的数据集基础上运行的？读文章的人是否能接触到文中所用的数据集？

全都是 CG 里的经典物体/场景了，比如 Cornell Box、Stanford bunny

8. 实验结果能否有力地支持假设？

可以。

  1. 微分结果上：无论是相同时间比质量，还是相同质量比时间，都是吊打以往的方法
  2. 逆向渲染上：传统方法会因高光处的噪声太多导致无法平滑的收敛，而加入了对偶渲染的技术之后，收敛的速度和结果都好很多

9. 这篇文章的贡献是什么？

作者发现对于高光表面，其BSDF函数往往在局部是偶函数，因此使用对偶采样可以加速蒙特卡洛采样的收敛速度，从而加快求导的速度。

10. 下一步可以做什么？

  1. 对偶采样与其他技术都是正交的，也就是说可以整合更多的前向渲染中的技术进来
  2. 对偶采样只解决了内部积分的问题，高光材质的边界积分估计还没被解决