1 导言
从现实世界中采集高精度的材质信息是一件非常重要而又非常具有挑战性的问题。这个问题可以被建模为空间变化的双向反射分布函数(SVBRDF)的采集,即一个六维的随位置、光照、视角变化而变化的函数。直接采集一个未知的 SVBRDF 函数需要上千张照片,因为你需要足够多的样本去涵盖所有可能的位置、光照、视角,这也直接导致了直接采集在时间和储存上的高成本。
为此,人们开展了很多关于提升采集效率的工作。一类主流的方法就是通过设计精巧的光照模式来实现采样的”并行化“,即在一次拍摄中尽可能采集更多的组合。但是即便是此前最好的解决方案(Guojun Chen, 2014. Reflectance Scanning: Estimating Shading Frame and BRDF with Generalized Linear Light Sources),也需要采集上百张照片。这使得这项技术在落地时仍然遇到巨大的困难。
为此,论文作者提出两个基于光照模式的反射采集方法的根本性问题:
- 在光照模式的数量有限的情况下,到底什么光照模式是最优的?
- 如何从这些模式下采集的照片中,还原出原本的物体?
以往的工作对于前两个问题的回答都是手工操作,也就是通过手工推导来设计各种复杂的光照模式,然后再解算出重建的方法。但是这样的方法有两个问题:1. 光照模式的数量往往取决于推导的方法,而无法任意根据所需的精度进行选择;2. 这些光照模式并没有在足够多的实际数据中进行其有效性的验证。
因此,论文作者选择使用数据驱动的方法,自动从大量真实物体的材质数据中学到最优的光照模式。
2 相关工作
2.1 直接采样
直接采样就是通过遍历 SVBRDF 的不同参数组合,来重建出整个 SVBRDF 函数。这一系列的工作精度非常的高,但工作量也非常的大,耗时很久,效率很低。
2.2 优化采样
这一方向主要是是增加假设来对于 BRDF 采样本身进行优化,比如 Matusik 等人通过假设一个任意的 BRDF 函数都落在一个预先捕捉好的各向同性的子空间中,成功将采样数量降低到了 800 张。而 Nielsen 等人通过一个能够优化光照和视角的改进算法,将采样数量降低到了 20 张。Xu 等人在 2016 年甚至通过在近场相机忽略掉视角的变化,将采样数降低到了 2 张,并通过假设表面没有法向的变化,将方法拓展到了各向同性的 SVBRDF 上。
2.3 复杂光照模式
但是增加假设的方法对于真实世界中的绝大多数情况都是不具有拓展性的,因此另一个方向是优化采集本身的效率。[Gardener et al. 2003; Ghosh et al. 2009; Aittala et al. 2013] 等三篇论文都尝试通过使用复杂的照明模式来实现光路复用,不过这几篇文章的作者都是手工设计的照明模式。
2.4 深度学习辅助的反射建模
[Aittala et al. 2016; Li et al. 2017] 两篇工作采用了深度学习来辅助反射建模。Aittala 等人使用单视角的闪光单张照片来建模各向同性的 SVBRDF 和表面法向。Li 等人的工作则能够使用未知的自然光照下的单张照片实现反射建模,通过一个基于 CNN 的网络,经过自增强训练,重建出材质的 SVBRDF 函数。
3 核心框架
3.1 问题形式化
3.1.1 假设条件
不失一般性,我们假设有一个近场光源,光源中的每一个点都可以被独立控制。装置被假设校准好且相机镜头不带偏振。需要采集的物体被假设为一个理想平面,而材质本身被表示为一个各向异性的 SVBRDF 函数,平面物体上的每个点需要进行独立的采集重建。
3.1.2 记号
此外我们需要定义一些记号:
| 记号 | 含义 |
|---|---|
| $x_p$ | 物体样本上 $p$ 点的位置 |
| $n_p$ | 物体样本上 $p$ 点的法向 |
| $x_l$ | 灯珠 $l$ 的位置 |
| $n_l$ | 灯珠 $l$ 的法向 |
| $\omega_i$ | 世界坐标系下光照方向 |
| $\omega_o$ | 世界坐标系下观察方向 |
| $\omega’_i$ | 物体坐标系下光照方向 |
| $\omega’_o$ | 物体坐标系下观察方向 |
| $I(l)$ | 灯珠 $l$ 的可编程亮度,取值范围 $[0, 1]$ |
| $\Psi$ | 描述灯珠在最大亮度时,亮度随角度的分布 |
| $f_r$ | 二维 BRDF 切片 |
| $\rho_d$ | 漫反射反照率 |
| $\rho_s$ | 镜面反射反照率 |
| $\alpha_x$ | 粗糙程度 |
| $\omega_h$ | 半向量方向 |
| $F$ | 菲涅耳系数 |
| $G_\text{GGX}$ | 阴影遮罩系数 |
| $B$ | 观测辐射值 |
| $m$ | Lumitexel 亮素 |
3.1.3 测量方程
这样我们就可以定义出特定光照下一点的辐射值:
$$ B(I, \mathbf{p})= \int \frac{1}{\left|\mathbf{x}{\mathbf{l}}-\mathbf{x}{\mathbf{p}}\right|^{2}} I(l) \Psi\left(\mathbf{x}{\mathbf{l}},-\omega_{\mathbf{i}}\right) f_{r}\left(\omega_{\mathbf{i}}^{\prime} ; \omega_{\mathbf{o}}^{\prime}, \mathbf{p}\right) \left(\omega_{\mathbf{i}} \cdot \mathbf{n}_{\mathbf{p}}\right)\left(-\omega_i\cdot n_l\right) d x_l $$
其中 $\omega_i$ 可以被表示为 $\omega_i=\frac{x_l-x_p}{\left|x_l-x_p\right|}$
3.1.4 BRDF 表示
BRDF 函数的表示形式选用了各向异性的 GGX BRDF 函数:
$$ f_{r}\left(\omega_{\mathrm{i}} ; \omega_{\mathbf{0}}, \mathbf{p}\right) = \frac{\rho_{d}}{\pi}+\rho_{s} \frac{D_{\mathrm{GGX}}\left(\omega_{\mathbf{h}} ; \alpha_{x}, \alpha_{y}\right) F\left(\omega_{\mathbf{i}}, \omega_{\mathbf{h}}\right) G_{\mathrm{GGX}}\left(\omega_{\mathbf{i}}, \omega_{\mathbf{o}} ; \alpha_{\mathbf{x}}, \alpha_{\mathbf{y}}\right)}{4\left(\omega_{\mathbf{i}} \cdot \mathbf{n}\right)\left(\omega_{\mathbf{0}} \cdot \mathbf{n}\right)} $$
作者选用 GGX 的考虑主要有以下三点:
- GGX 是一个参数化模型,且非常“紧凑”,能够表示非常广泛的材料
- GGX 已经是 PBR (基于物理渲染)的行业标准
- GGX 能够实现高效的实时渲染
3.1.5 Lumitexel
亮素(亮光像素),其实就是将物体的每一个点视为一个 pixel,然后在上面储存该点在不同方向光照下的高光数据。
作者在 slide 里的插图对于 Lumitexel 给出了比较形象的展示:
Lumitexel 本身是一个物体的客观属性,标记了物体上的一个点在受到来自某个单一方向的标准亮度光照照射时,所反射出来的光线亮度
将 Lumitexel 与实际的光照模式直接相乘,就得到了采集到的测量结果
Lumitexel 形式化表示如下: $$ m(j ; \mathbf{p})=B({I(l=j)=1, I(l \neq j)=0}, \mathbf{p}) $$ 而观测到的辐射值在物理上其实就是 Lumitexel 与照明模式的点积: $$ B(I, \mathrm{p})=\sum_{l} I(l) m(l ; \mathrm{p}) $$
3.1.6 问题定义
物体材质的采集本质就是在给定物体某一点 $\text{p}$ 的参数 ${\rho_d, \rho_s, \alpha_x, \alpha_y, \text{n}, \text{t}}$ 、一批光照模式 ${I(l\text{p})}_I$ 以及对应光照模式下实际采集到的辐射值 ${B(I, \text{p})}_I$ ,求解一个未知的 BRDF 函数 $f_r$。
3.2 求解思路与工作框架
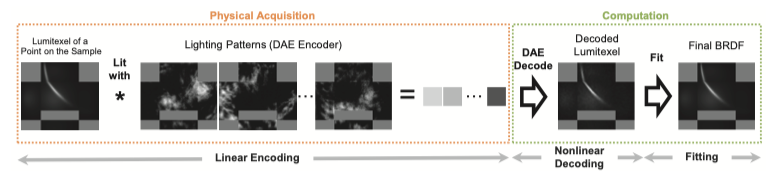
问题的本质其实已经在形式化部分给出,简单来说就是下面这张图所需要解的问题:
其中最左边的 Lumitexel 是未知但固有存在的物理属性,中间的光照模式是需要设计的,测量值是客观测量出来的,而最右边的 BRDF 是要求解的。
而这本质是一个编码解码的过程:光照是对物体材质属性的物理编码,而求解就是一个解码过程,可以概括为下图:
以往的方法无论是光照模式还是解码方式,都是手工设计的——这样会带来两个问题:模式不一定最优且模式数量难以降低,进而导致了采样效率低下。于是文章的作者创新性地提出可以使用网络来自动优化出最合适的编码解码方式。
一般来说,最直接的想法是解码器直接从观测值拟合到 BRDF 函数。这一设计非常端到端,但是作者意识到这个映射并不是一个单射关系,而是一个一对多的关系——一个实际的物体其实可以被多组 BRDF 参数描述,典型的就是假如某一点的镜面反射率为 0,那么在法向和漫反射率确定的情况下,其他参数可以任意变化;再比如 BRDF 中的切向 tangent 值可以为正也可以为负,而不影响其含义。这种性质对于回归模型非常不友好。
因此,作者决定使用自编码器 AutoEncoder,来规避这种一对多的关系;而如果对 BRDF 本身进行自编码,会需要引入相机的视角等信息,从而增加网络的复杂度,而且模型会与 BRDF 形式的耦合,每更换一个 BRDF 函数就需要重新训练整个网络;另一方面,从 Lumitexel 到 BRDF 的拟合方法已经非常成熟,并不需要用网络就可以完成;由此作者直接选用 Lumitexel 作为自编码的对象,提出了下面的工作流程:
3.3 模型结构与损失函数
3.3.1 L-DAE
作者把这个自编码 Lumitexel 的网络称为 L-DAE (Lumitexel Deep AutoEncoder)。
对于 L-DAE 的编码器部分,作者将所有的照明模式视为一个 $c \times 1 \times \sharp$ 的卷积核,其中 $c$ 是 Lumitexel 的维度,而 $\sharp$ 代表光照模式的个数。这是硬件设计所产生的约束——每个卷积核的权重都对应了一颗灯珠在一种照明模式下的亮度,所以编码器必须是线性的。不过由于输入的 Lumitexel 维度其实与卷积核的第一个维度一样,整个卷积层其实与一个全连接层是等价的。
而对于解码器部分,由于它是直接运行在计算设备上而非物理采集设备上,所以没有任何的限制。于是作者决定不加入任何假设和先验知识,直接使用 11 层全连接层,构造出一个非线性的解码器。使得解码器能够实现非常复杂的解码任务。
完整的网络结果如下图所示:
3.3.2 损失函数
L-DAE 的损失函数包含了两个部分:自编码器的解码误差与 Lumitexel 物理意义上的硬性约束。 $$ L=L_{\text {auto }}(m)+\lambda \sum_{w \in \text { enc. }} L_{\text {barrier }}(w) $$ 自编码器的误差就是输入的 Lumitexel 与重建出来的 Lumitexel 的差异: $$ L_{\text {auto }}(m)=\sum_{j}\left[\log (1+m(j))-\log \left(1+m_{\mathrm{gt}}(j)\right)\right]^{2} $$ 注意到作者引入了 $log$ 来缓解镜面反射所带来的高光对于损失造成过大的影响。
而由于 Lumitexel 每个值的取值范围都应当在 $[0, 1]$ 之间,作者引入了一个 barrier 损失来刻画对于超出物理取值范围的点的惩罚: $$ L_{\text {barrier }}(w)=\tanh \left(\frac{w-(1-\epsilon)}{\epsilon}\right)+\tanh \left(\frac{-w+\epsilon}{\epsilon}\right)+2 $$ 在实验中,作者发现 $\lambda=0.03, \epsilon=0.005$ 是一组不错的参数。
4 采集实验
为了验证方法的可行性,作者进行了真实的采集实验。
4.1 设备搭建
作者首先搭建了一个近场 lightstage (我也不知道中文这个叫啥好,英文非常形象)。lightstage 的底部放置了要采集的平面物体,其他五面环绕了 LED 灯板,如下如所示:
将灯板展开后,我们可以得到下面的图示:
与所有的采集装置一样,整个 lightstage 对相机的内参外参畸变参数、以及灯板的位置进行了校准,得到了精确的空间位置关系。
另外为了实现相机快门与 LED 光照模式的同步,作者使用了 Altera(Intel) 的 Cyclone FPGA 进行高精度控制。亮度上使用了 8-bit 进行刻画,可以描述 256 种不同的亮度。由于装置是近场装置,不同角度与距离对于灯珠光线的衰减影响可以忽略不计。LED 的灯珠颜色使用了 X-Rite 校色仪进行修正。漫反射与镜面反射的尺度模糊问题使用了一个平面均匀漫反射贴片来解决。
4.2 模型训练
作者使用纹理生成的方法,利用大量真实世界的物体数据,结合装置的校准结果,随机采样生成了 1,000,000,000 (1 million) 个 Lumitexel,然后交给网络进行训练。
网络使用了 RMSProp 作为优化器;对于编码器的权重使用了正太分布进行初始化,并翻转了为负的权重;对于解码器,使用了 xavier 算法进行初始化。
4.3 其他实现细节
所有输入的 Lumitexel 都被减去了均值——感觉在机器学习里这是个常规操作了,不管是 PCA 还是其他降维的方法。在物理采集的时候,这个均值会乘上光照模式后在采样结果上减去,然后经过解码之后再加上。
BRDF 的拟合上,作者使用了一个各向异性的 GGX 模型,并使用 Levenberg-Marquardt 算法来对参数拟合出来的结果与实际结果的方差进行优化。
5 实验结果
5.1 时间消耗
网络的训练大约持续了 5 小时;训练好的模型编码速度(硬件采集拍摄)大概在 12~25 秒(取决于材质所需的曝光时间以及选用的光照模式数量);每 1M 大小的 Lumitexel 大约需要 4 分钟解码和 1.6 小时来进行最后的 BRDF 拟合。
5.2 光照模式
将模型学习到的线性编码器的每一个模式可视化出来,可以得到下面的一张图:图片从上到下每一列分别是各向异性样本的学习结果、各向同性样本的学习结果、PCA 降维直接得到的结果。可以明显看到这些光照模式都非常复杂,不是人能轻易设计出来的;而模型学习出来的模式是最复杂的。
5.3 拍摄结果
使用训练出来的光照模式进行采集拍摄,所有的拍摄照片使用两张 SDR 照片合成出一张 HDR 照片,以获得更广泛的亮度范围。
将不同的光照模式拍摄得到的照片与光照模式一起并排放置,可以得到下面的结果:
可以看到,每一张照片看起来都非常不同,这也充分说明这一方法采集的效率之高,在很少的几张照片里涵盖了尽可能多的信息。
5.4 重建结果
经过非线性解码和 BRDF 拟合,可以得到下面的重建结果:
其中最后一行是重建结果与 ground truth 的差异,可以看到差异非常的小,说明这一方法的采集精度也非常的高。
5.5 对比实验
5.5.1 降维策略对比
对比 DAE 编码器+非线性解码器、PCA 编码器 + 非线性解码器、DAE 编码器 + 线性解码器、PCA 编码器 + 非线性解码器,可以看到 DAE 编码器+非线性解码器的重建结果是最好的。
5.5.2 光照模式数量的影响对比
调整光照模式的数量,可以看到数量越多,模型训练的 loss 越小,重建效果也越好。
重建结果也映证了这一点:
5.5.3 鲁棒性
作者增加了不同的高斯噪声,来模拟拍摄时引入的噪声。拟合结果显示这一方法对于不同程度的噪声都表现出很强的抵抗性。
5.5.4 训练数据集分布
作者还对比了对于某一个给定的样本,使用不同的训练数据会对采样效率产生什么样的影响。从左到右分别是基准方法(直接采样)、使用了各向异性的样本、使用了各向同性的样本、以及将待采集的样本放入训练集中所需要的光照模式数量。
可以看出,为了达到相同的重建效果,预设的信息越多、需要采集的信息就越少、从而使得光照模式数量变少。
6 局限和展望
这一方法有以下局限:
由于使用了数据驱动的编码器设计方法,所以在面对与数据集显著不同的数据时,模型的重建结果会非常的差,比如下图中的双向高光,就难以被重建:
这一方法现在还是只能采集平面物体
这一方法目前只利用到了一个视角
不过作者在后一年的 SIGGRAPH Asia 19 上的论文解决了后两个问题,实现了基于多视角的立体物体的采集重建。
未来作者表示还会尝试适配这套方法到远场 lightstage、相机视角设计、以及基于图片的重光照问题。